Френелови интеграли

Френелови интеграли Не можев да расчленам (SVG (MathML може да се овозможи преку приклучок на прелистувачот): Неважечки одговор („Math extension cannot connect to Restbase.“) од опслужувачот „http://localhost:6011/mk.wiki.x.io/v1/“:): {\displaystyle S(x)} и Не можев да расчленам (SVG (MathML може да се овозможи преку приклучок на прелистувачот): Неважечки одговор („Math extension cannot connect to Restbase.“) од опслужувачот „http://localhost:6011/mk.wiki.x.io/v1/“:): {\displaystyle C(x)} - математички трансцендентни функции кои Огистен-Жан Френел ги користел во оптиката. Се користат да ја опишат Френеловата дифракција, а се дефинирани со следните интеграли:

Не можев да расчленам (SVG (MathML може да се овозможи преку приклучок на прелистувачот): Неважечки одговор („Math extension cannot connect to Restbase.“) од опслужувачот „http://localhost:6011/mk.wiki.x.io/v1/“:): {\displaystyle S(x)=\int_0^x \sin(t^2)\,dt,\quad C(x)=\int_0^x \cos(t^2)\,dt.}

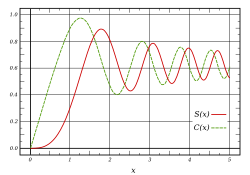
Со истовремен параметарски цртеж на двата интеграла се добива Ојлерова спирала.

Дефиниција

Не можев да расчленам (SVG (MathML може да се овозможи преку приклучок на прелистувачот): Неважечки одговор („Math extension cannot connect to Restbase.“) од опслужувачот „http://localhost:6011/mk.wiki.x.io/v1/“:): {\displaystyle S(x)=\int_0^x \sin(t^2)\,dt=\sum_{n=0}^{\infin}(-1)^n\frac{x^{4n+3}}{(2n+1)!(4n+3)},}

Не можев да расчленам (SVG (MathML може да се овозможи преку приклучок на прелистувачот): Неважечки одговор („Math extension cannot connect to Restbase.“) од опслужувачот „http://localhost:6011/mk.wiki.x.io/v1/“:): {\displaystyle C(x)=\int_0^x \cos(t^2)\,dt=\sum_{n=0}^{\infin}(-1)^n\frac{x^{4n+1}}{(2n)!(4n+1)}.}

Некои автори го користата Не можев да расчленам (SVG (MathML може да се овозможи преку приклучок на прелистувачот): Неважечки одговор („Math extension cannot connect to Restbase.“) од опслужувачот „http://localhost:6011/mk.wiki.x.io/v1/“:): {\displaystyle \frac{\pi}{2}t^2} како аргумент во интегралот при дефинирање на Не можев да расчленам (SVG (MathML може да се овозможи преку приклучок на прелистувачот): Неважечки одговор („Math extension cannot connect to Restbase.“) од опслужувачот „http://localhost:6011/mk.wiki.x.io/v1/“:): {\displaystyle S(x)} и Не можев да расчленам (SVG (MathML може да се овозможи преку приклучок на прелистувачот): Неважечки одговор („Math extension cannot connect to Restbase.“) од опслужувачот „http://localhost:6011/mk.wiki.x.io/v1/“:): {\displaystyle C(x)} . Тогаш интегралите се множат со Не можев да расчленам (SVG (MathML може да се овозможи преку приклучок на прелистувачот): Неважечки одговор („Math extension cannot connect to Restbase.“) од опслужувачот „http://localhost:6011/mk.wiki.x.io/v1/“:): {\displaystyle \sqrt{\frac{2}{\pi}}} , а аргументот x со Не можев да расчленам (SVG (MathML може да се овозможи преку приклучок на прелистувачот): Неважечки одговор („Math extension cannot connect to Restbase.“) од опслужувачот „http://localhost:6011/mk.wiki.x.io/v1/“:): {\displaystyle (\frac{\pi}{2})^{1/2}} .

Ојлерова спирала

Ојлеровата спирала е позната и како Корнуова спирала или клотоида, а се добива со параметарски приказ на Не можев да расчленам (SVG (MathML може да се овозможи преку приклучок на прелистувачот): Неважечки одговор („Math extension cannot connect to Restbase.“) од опслужувачот „http://localhost:6011/mk.wiki.x.io/v1/“:): {\displaystyle S(t)} спрема Не можев да расчленам (SVG (MathML може да се овозможи преку приклучок на прелистувачот): Неважечки одговор („Math extension cannot connect to Restbase.“) од опслужувачот „http://localhost:6011/mk.wiki.x.io/v1/“:): {\displaystyle C(t)} . Со помош на дефинициите на Френеловите интеграли за dx и dy се добива:

Не можев да расчленам (SVG (MathML може да се овозможи преку приклучок на прелистувачот): Неважечки одговор („Math extension cannot connect to Restbase.“) од опслужувачот „http://localhost:6011/mk.wiki.x.io/v1/“:): {\displaystyle dx = C'(t)dt = \cos(t^2) dt \,}

Не можев да расчленам (SVG (MathML може да се овозможи преку приклучок на прелистувачот): Неважечки одговор („Math extension cannot connect to Restbase.“) од опслужувачот „http://localhost:6011/mk.wiki.x.io/v1/“:): {\displaystyle dy = S'(t)dt = \sin(t^2) dt \,}

Должината на спиралата мерена од извориштето може да се претстави како:

Не можев да расчленам (SVG (MathML може да се овозможи преку приклучок на прелистувачот): Неважечки одговор („Math extension cannot connect to Restbase.“) од опслужувачот „http://localhost:6011/mk.wiki.x.io/v1/“:): {\displaystyle L = \int_0^t {\sqrt {dx^2 + dy^2}} = \int_0^t{dt} = t }

Својства

Не можев да расчленам (SVG (MathML може да се овозможи преку приклучок на прелистувачот): Неважечки одговор („Math extension cannot connect to Restbase.“) од опслужувачот „http://localhost:6011/mk.wiki.x.io/v1/“:): {\displaystyle S(x)} и Не можев да расчленам (SVG (MathML може да се овозможи преку приклучок на прелистувачот): Неважечки одговор („Math extension cannot connect to Restbase.“) од опслужувачот „http://localhost:6011/mk.wiki.x.io/v1/“:): {\displaystyle C(x)} се непарни функции
Френеловите интеграли можат да се изразат преку функцијата на грешка Не можев да расчленам (SVG (MathML може да се овозможи преку приклучок на прелистувачот): Неважечки одговор („Math extension cannot connect to Restbase.“) од опслужувачот „http://localhost:6011/mk.wiki.x.io/v1/“:): {\displaystyle \operatorname{erf}(x)} :

Не можев да расчленам (SVG (MathML може да се овозможи преку приклучок на прелистувачот): Неважечки одговор („Math extension cannot connect to Restbase.“) од опслужувачот „http://localhost:6011/mk.wiki.x.io/v1/“:): {\displaystyle S(x)=\frac{\sqrt{\pi}}{4} \left(\sqrt{i}\,\operatorname{erf}(\sqrt{i}\,x) + \sqrt{-i}\,\operatorname{erf}(\sqrt{-i}\,x) \right)}

Не можев да расчленам (SVG (MathML може да се овозможи преку приклучок на прелистувачот): Неважечки одговор („Math extension cannot connect to Restbase.“) од опслужувачот „http://localhost:6011/mk.wiki.x.io/v1/“:): {\displaystyle C(x)=\frac{\sqrt{\pi}}{4} \left(\sqrt{-i}\,\operatorname{erf}(\sqrt{i}\,x) + \sqrt{i}\,\operatorname{erf}(\sqrt{-i}\,x) \right).}

Интегралите не можат да се пресметаат во затворена форма со помош на елементарни функции, освен во специјални случаи. Како x тежи кон бесконечност се добива:

Не можев да расчленам (SVG (MathML може да се овозможи преку приклучок на прелистувачот): Неважечки одговор („Math extension cannot connect to Restbase.“) од опслужувачот „http://localhost:6011/mk.wiki.x.io/v1/“:): {\displaystyle \int_{0}^{\infty} \cos t^2\,dt = \int_{0}^{\infty} \sin t^2\,dt = \frac{\sqrt{2\pi}}{4} = \sqrt{\frac{\pi}{8}}.}

Генерализација

Не можев да расчленам (SVG (MathML може да се овозможи преку приклучок на прелистувачот): Неважечки одговор („Math extension cannot connect to Restbase.“) од опслужувачот „http://localhost:6011/mk.wiki.x.io/v1/“:): {\displaystyle \int_0^\infty\sin(x^a)\ dx = \frac{\Gamma\left(\frac{1}{a}\right)\sin(\frac{\pi}{2a})}{a}}

Литература

Abramowitz, Milton; Stegun, Irene A., eds. , Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, New York: Dover. Френелови интеграли
Френелови интеграли

Надворешни врски

Cephes, Free and open-source software C++/C code to compute Fresnel integrals among other special functions. Used in SciPy and ALGLIB.
Faddeeva Package, Free and open-source software C++/C code to compute complex error functions (from which the Fresnel integrals can be obtained), with wrappers for Matlab, Python, and other languages.
Хацевинкел, Михил, уред. (2001), „Fresnel integrals“, Математичка енциклопедија, Шпрингер, ISBN 978-1556080104
„Roller Coaster Loop Shapes“. Архивирано од изворникот на September 23, 2008. Посетено на 2008-08-13.
„Fresnel Integrals“ од Ерик В. Вајсштајн — MathWorld (англиски)

„Cornu Spiral“ од Ерик В. Вајсштајн — MathWorld (англиски)